Renditeprognosen im Niedrigzinsumfeld
Feb 2017
Welche Renditen können Anlageklassen im Niedrigzinsumfeld erwirtschaften und wie sieht ein optimales Portfolio aus? Dieser Frage wollen wir anhand eines einfachen Beispielportfolios aus Staats- und Unternehmensanleihen nachgehen. Wir wollen zeigen, dass direkt aus der Vergangenheit abgeleitete Renditeprognosen falsche Ergebnisse und Fehlallokationen produzieren, und dem gegenüber unseren Ansatz darstellen.
1. Ausgangssituation
Die zentrale Frage der Asset Allokation betrifft die Verteilung der Anlagegelder auf die zur Verfügung stehenden Anlageklassen. Dazu bedarf es einer Prognose, wie sich die Renditen und Schwankungsbreiten (Volatilitäten) der jeweiligen Anlageklassen im Prognosezeitraum (häufig ein Jahr) entwickeln werden und wie die Anlageklassen miteinander korrelieren. Unser Beispielportfolio soll zu Demonstrationszwecken nur aus zwei Anlageklassen bestehen:
– 5-jährige US-Staatsanleihen (nachfolgend „Treasuries“ genannt)
– 5-jährige US-Unternehmensanleihen mit einem Rating von BBB/Baa (nachfolgend „Corporate Bonds“ genannt)
Die jährlichen Gesamterträge der beiden Anlageklassen lassen sich in Kupon- und Kurserträge aufspalten und sahen in den vergangenen Jahren in etwa wie folgt aus:
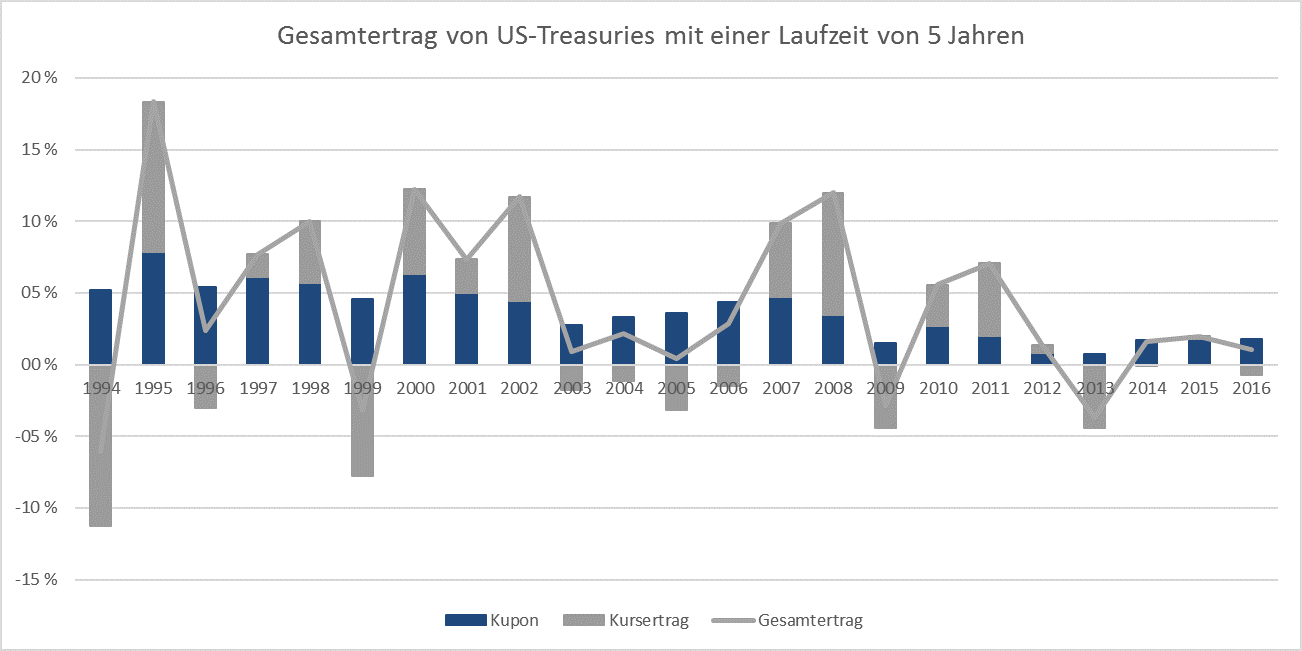
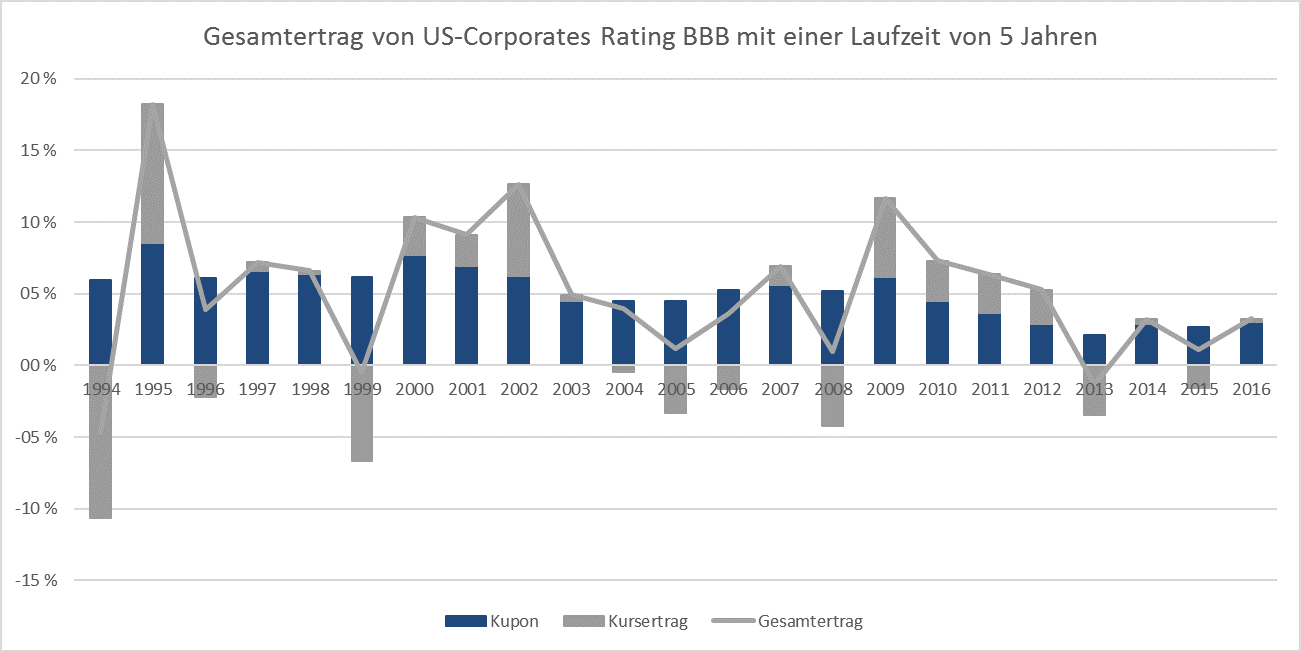(US-Corporate Bonds wurden um Downgrades und Defaults „bereinigt“)
2. Der traditionelle Ansatz in der Asset Allokation
In einem häufig verwendeten Ansatz werden für die Prognose der Renditen und Schwankungsbreiten (Volatilitäten) einfach die Durchschnittswerte aus der Vergangenheit herangezogen. Dabei wird die Gewichtung der jeweiligen Anlageklassen im Portfolio von null bis hundert Prozent variiert, so dass die Summe immer 100% ergibt, das Portfolio also jeweils voll investiert ist. Für das jeweilige Kombinationsportfolio wird die Rendite und Schwankungsbreite anhand der historischen Datenreihen berechnet und in einem Rendite-/Standardabweichung-Schaubild dargestellt. Da die Korrelationen der Anlageklassen meist kleiner als eins sind, ergibt sich aus den verschiedenen Kombinationsvariationen in diesem Schaubild keine Gerade, sondern eine Kurve, deren äußerster (oberster) Rand auch als effiziente Grenze („Efficient Frontier“) bezeichnet wird.
In unserem Beispiel haben wir Treasuries und Corporate Bonds in 10%-Schritten kombiniert (also 0% Treasuries/100% Corporate Bonds, 10%/90%, 20%/80%, usw.) und den Mittelwert für die jährlichen Portfoliorenditen und -standardabweichungen seit 1994 berechnet:
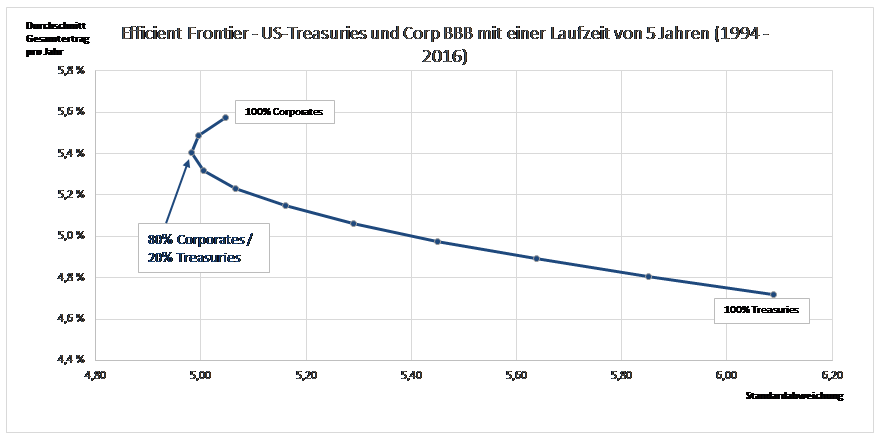
Überraschend scheint beim Blick auf das Schaubild zunächst einmal, dass in dem gewählten Zeitraum von 1994 bis 2016 Corporate Bonds mit einem Rating von BBB eine geringere Standardabweichung und eine höhere Durchschnittsrendite aufweisen als Treasuries. Dies lässt sich durch mindestens zwei Faktoren erklären:
Zum einen bot dieser Zeitraum trotz der Finanzkrise von 2008/2009 ein besonders günstiges Umfeld für Unternehmen (Globalisierung, Liberalisierung, Deregulierung, Flexibilisierung des Arbeitsmarktes, etc.).
Zum anderen setzen sich die Renditen von Unternehmensanleihen im Wesentlichen aus zwei Risikokomponenten zusammen. Diese zwei Risikokomponenten, Zins und Spread (Risikoaufschlag), wirken bei Unternehmensanleihen generell stabilisierend, da in einem günstigen (ungünstigen) Wirtschaftsumfeld steigende (fallende) Zinsen oft mit fallenden (steigenden) Spreads einhergehen und daher risiko- bzw. schwankungsmindernd wirken, die zwei Risikokomponenten Zins und Spread mithin also negativ korreliert sind.
Bereits hieran sieht man, dass das Verhalten einer Anlageklasse innerhalb eines bestimmten Zeitraums von besonderen Umständen abhängt, die bei einer Prognose berücksichtigt werden sollten.
Kehren wir zurück zu der Frage, wie ein Investor aus diesen beiden Anlageklassen nun ein optimales Portfolio zusammenstellt. Ein risikoscheuer Investor, der sich an dieser so berechneten effizienten Grenze orientiert und annimmt, dass die Vergangenheit ein guter Anhaltspunkt für die Zukunft ist, legt nach gängiger Portfoliotheorie 20% seines Portfolios in Treasuries und 80% in Corporate Bonds an. Er geht davon aus, dass eine solche Kombination der beiden Anlageklassen das effizienteste Portfolio (ohne Kassenhaltung) darstellt.
3. Berücksichtigung der Anleihearithmetik und der momentan niedrigen Kupons/Renditen
Allerdings werden bei diesem gängigen Ansatz die momentan niedrigen Renditen und die Arithmetik für Anleihen völlig außer Acht gelassen. Denn die Performance von Anleihen folgt klaren Regeln und setzt sich wie folgt zusammen:
Gesamtertrag = Kuponertrag + Kursgewinn/-verlust – sonstiger Verlust
Um den Gesamtertrag zu prognostizieren, benötigt man also Schätzungen für die drei Bestandteile Kuponertrag, Kursentwicklung und sonstige Verluste.
Kuponertrag: Der Kupon einer Anleihe steht bei Kauf fest und muss daher nicht prognostiziert werden. Für 5-jährige Treasuries beträgt er momentan ca. 1,95%. Für Corporate Bonds mit einem Rating von BBB gibt es darauf noch einen Risikoaufschlag (Spread) von 0,89%, so dass dort der Kupon (und die Rendite bei einem Preis von 100%) rund 2,84% beträgt.
Kursgewinn/-verlust: Die Kursentwicklung hängt davon ab, wie sich die Anleiherenditen und -spreads im Prognosezeitraum verändern. Generell lässt sich die Kursentwicklung annäherungsweise durch die folgende Formel berechnen:
Kursgewinn/-verlust = Modified Duration (am Ende des Prognosezeitraums) x -Veränderung der Renditen/Spreads (im Prognosezeitraum)
Sonstige Verluste: Bei Anleihen mit einem Ausfallrisiko („Credits“) müssen darüber hinaus noch weitere mögliche Verluste, die durch Unternehmensausfälle („Defaults“) oder Ratingverschlechterungen entstehen, modelliert werden. Bei Anleihen mit einem Investmentgrade-Rating (Rating BBB oder besser) kommen direkte Unternehmensausfälle (in einem breit diversifizierten Portfolio) recht selten vor, die sonstigen Verluste werden dort hauptsächlich durch einen Anstieg der Risikoaufschläge („Spreads“) aufgrund von Ratingverschlechterungen verursacht. Sowohl Unternehmensausfälle als auch Ratingverschlechterungen weisen aber zu den zu modellierenden Spreadveränderungen (siehe oben) eine hohe Korrelation auf, wie auch das folgende Schaubild zeigt:
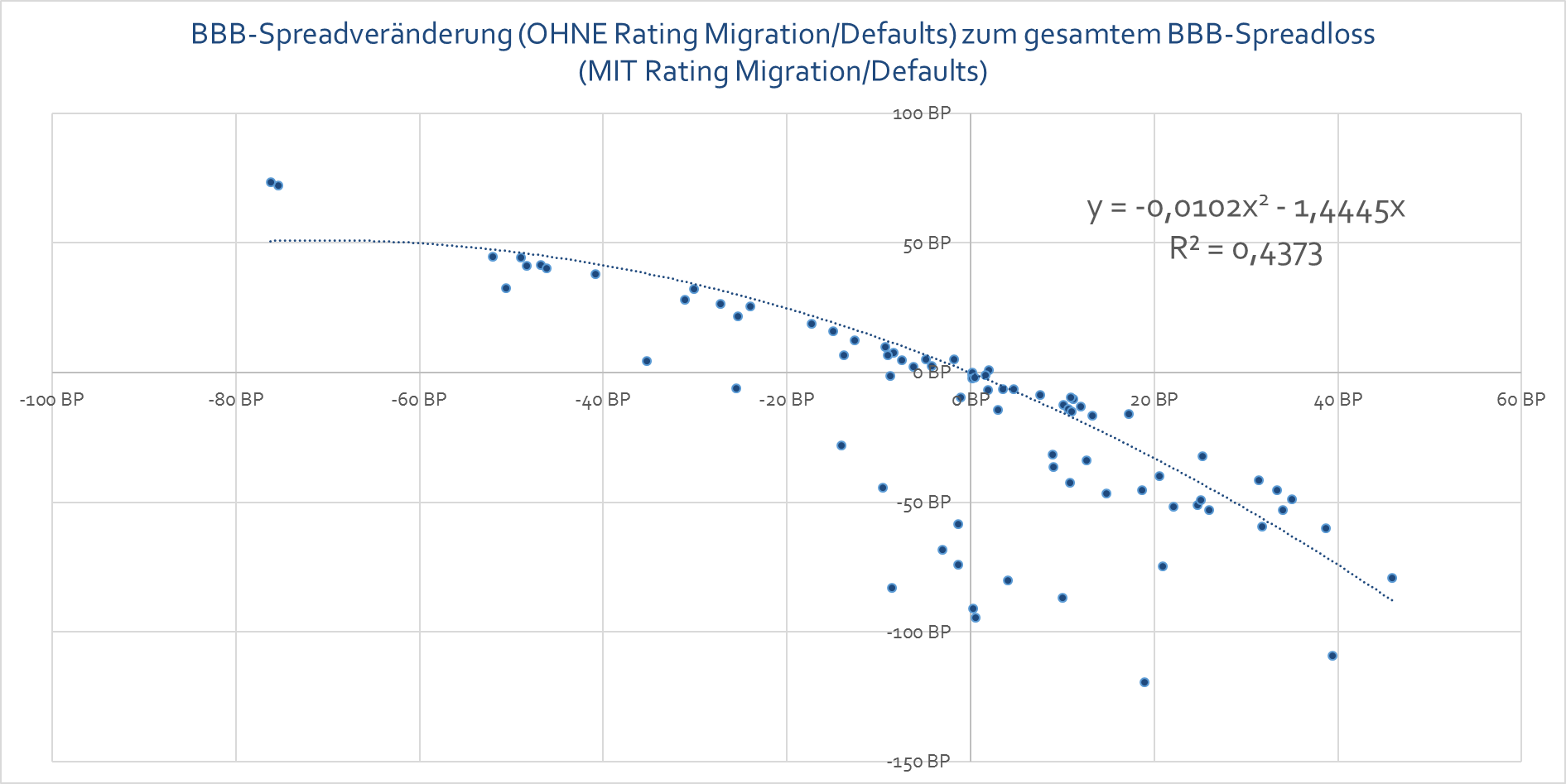
Sie werden von uns in der Beratungspraxis in den Veränderungen der Spreads und damit bei den Kursgewinnen/-verlusten (siehe oben) berücksichtigt. In unserem Beispiel hier wollen wir darauf aus Vereinfachungsgründen aber nicht weiter eingehen, ebenso wenig wie auf den Konvexitätseinfluss und die Ungenauigkeit der Durationsprognose für das Ende des Prognosezeitraums. Den Kursgewinn/-verlust berechnen wir nun also wie folgt:
Kursgewinn/-verlust = Modified Duration (am Ende des Prognosezeitraums) x -Veränderung der Renditen/Spreads (im Prognosezeitraum und inklusive Defaults und Ratingveränderungen)
Die „Modified Duration“ drückt die Preissensitivität im Hinblick auf Rendite- und Spreadveränderungen aus und ist für das Ende des Prognosezeitraums, in unserem Fall in einem Jahr, relativ genau vorhersagbar. Für unser Beispiel haben wir folgende Werte angenommen:
Modified Duration für 4-jährige Treasuries: 3,9
Modified Duration für 4-jährige Corporate Bonds: 3,7
Die Laufzeit hat sich am Ende des einjährigen Prognosezeitraums auf vier Jahre verkürzt, die Modified Duration (und auch die Rendite-/Spreadveränderungen) muss sich also auf vierjährige Anleihen beziehen. Zur Berechnung des Gesamtertrags fehlt also nur noch die Prognose, wie sich die Spreads und Renditen der Anleihen über den Prognosezeitraum – in unserem Beispiel ein Jahr – entwickeln werden.
Wie prognostiziert man nun die Veränderungen von Renditen und Spreads? Richten wir einen Blick auf die historischen (jährlichen) Veränderungen von Renditen und Spreads der für unser Beispiel relevanten Anlageklassen:
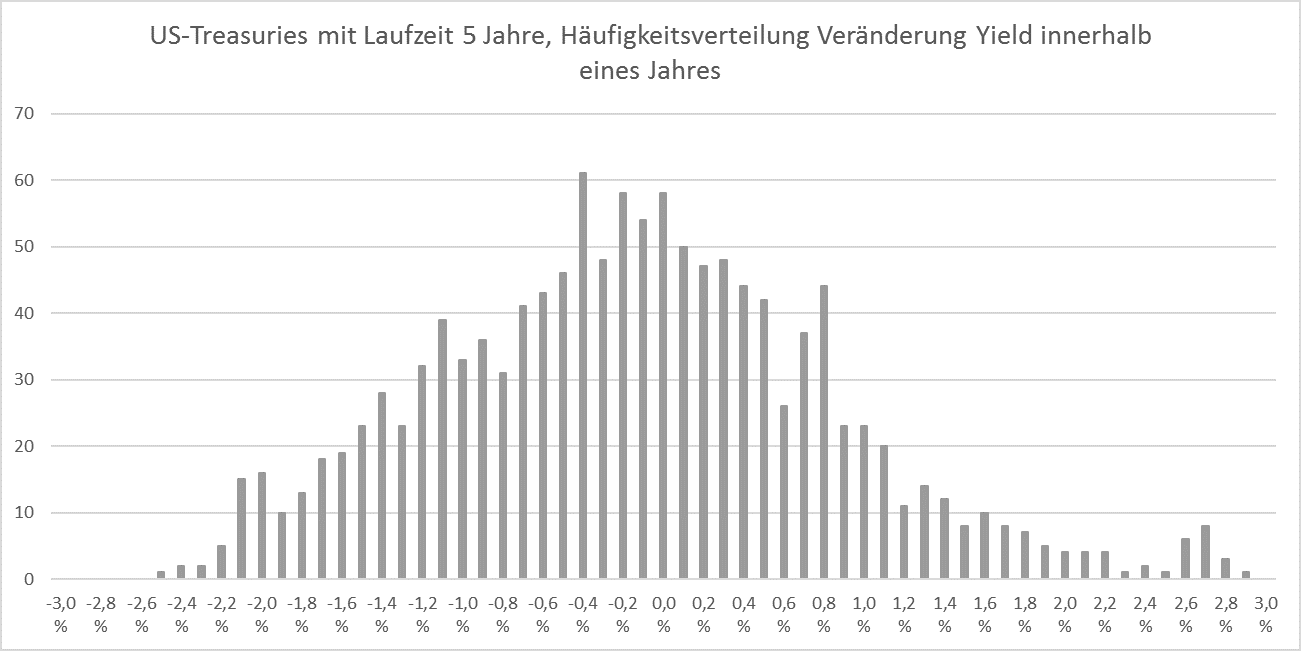
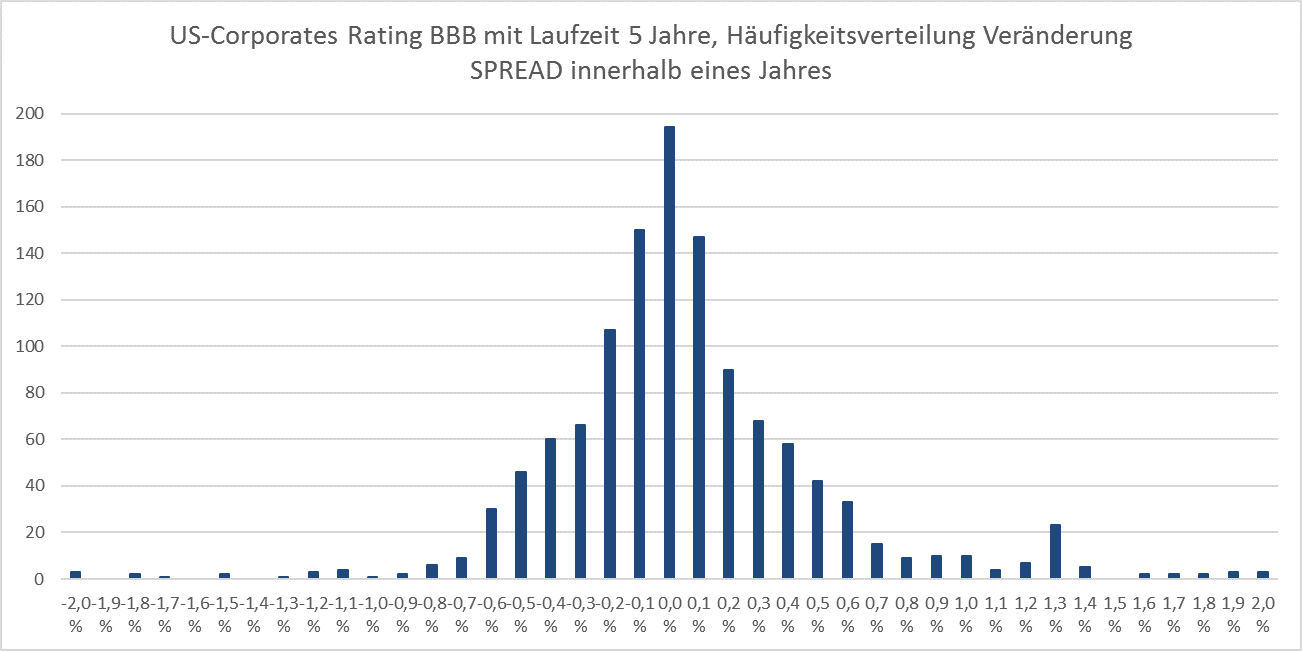
Können diese historischen Rendite- und Spreadveränderungen als Anhaltspunkt für die Zukunft dienen? Ja! Denn Untersuchungen zeigen, dass die Rendite-/Spreadveränderungen im Gegensatz zu den Gesamterträgen historisch stabil und mit hoher Wahrscheinlichkeit normalverteilt sind. Für die Prognose des Gesamtertrags der beiden Anlageklassen stehen uns nun alle Variablen zur Verfügung. Die wahrscheinlichen Renditen und Schwankungsbreiten der beiden Anlageklassen unter Berücksichtigung der gegenwärtig niedrigen Kupons und Renditen berechnen wir nun wie folgt:
Gesamtertrag Anleihen = Kuponertrag + (Modified Duration x – historische Veränderung der Renditen/Spreads)
Gesamtertrag Treasuries = 1,95% – (3,9 x historische Renditeveränderung Treasuries)
Gesamtertrag Corporate Bonds = 2,84% – 3,7 x (historische Renditeveränderung Treasuries + historische Spreadveränderung Corporate Bonds)
Wir setzen also die historischen Rendite- und Spreadveränderungen (plus einem Korrektiv für die Defaults und Ratingveränderungen bei Corporate Bonds, wie oben beschrieben) in diese Formeln ein und erhalten für die beiden Anlageklassen ein Spektrum der theoretisch wahrscheinlichen Gesamterträge und Schwankungsbreiten (Volatilitäten). Daraus lassen sich nun wieder Kombinationsportfolien nach obigem Muster (also 0% Treasuries/100% Corporate Bonds, 10%/90%, 20%/80%, usw.) und eine effiziente Grenze berechnen. Dieser Ansatz hat gegenüber dem rein historischen Ansatz von oben den Vorteil, dass hierbei die momentan niedrigen Kupons berücksichtigt werden und die Renditeprognosen somit realistischer sind.
4. Berücksichtigung der möglichen Rendite- und Spreadveränderungen
Eine noch bessere Prognose erhalten wir aber, wenn wir auch die möglichen Veränderungen der Renditen und Spreads an den momentanen Marktgegebenheiten ausrichten. Nimmt man beispielsweise an, dass die Spreads von 4-jährigen Corporate Bonds nicht unter 0,40% und dass die Rendite von 4-jährigen Treasuries nicht unter 0,00% sinken wird, dann können die Renditen von Treasuries in unserem Beispiel nur noch um 1,95% absinken und die Spreads von Corporate Bonds sich nur noch um 0,49% einengen. Selbstverständlich können für die unteren Grenzen auch andere Werte angenommen werden.
Extremveränderungen der Renditen und Spreads nach unten wie in der Vergangenheit, sind nun also nicht mehr im selben Ausmaß möglich. Und diese Grenzen haben Auswirkungen auf die möglichen Kursveränderungen und damit eben auch auf die erzielbaren Gesamtrenditen.
Aufgrund dieser Untergrenzen ergibt sich ein modifiziertes Spektrum von Rendite- und Spreadveränderungen:
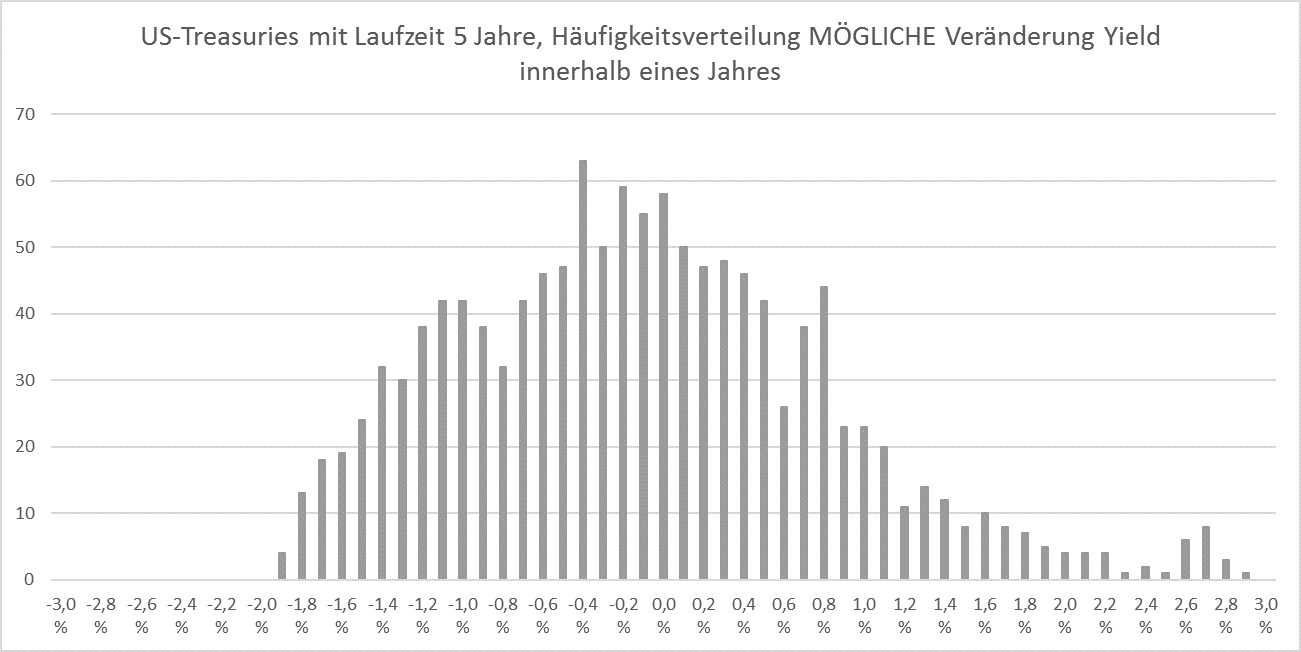
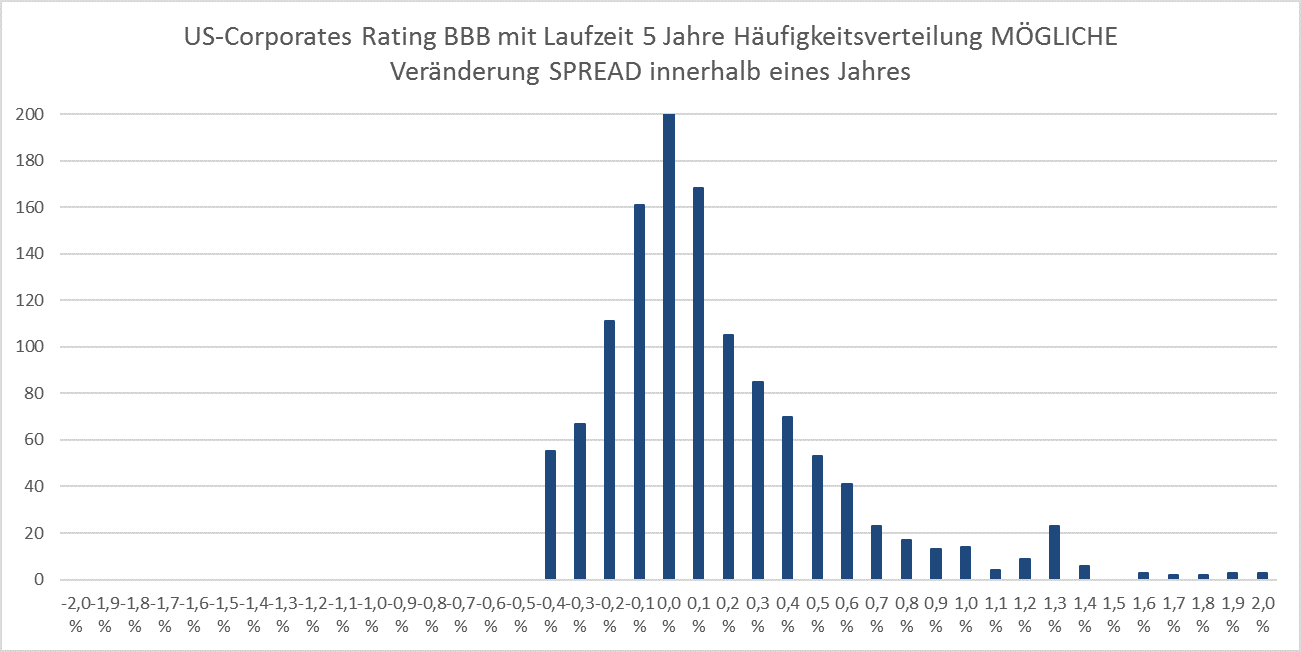
Aufgrund dieser modifizierten Rendite- und Spreadveränderungen, die wir MÖGLICHE Veränderungen nennen wollen, ergeben sich auch Veränderungen für die Berechnung der Gesamterträge. Die modifizierte Formel lautet nun:
Gesamtertrag Anleihen = Kuponertrag + (Modified Duration x – MÖGLICHE Veränderung der Renditen/Spreads)
Gesamtertrag Treasuries = 1,95% – (3,9 x MÖGLICHE Renditeveränderung Treasuries)
Gesamtertrag Corporate Bonds = 2,84% – 3,7 x (MÖGLICHE Renditeveränderung Treasuries + MÖGLICHE Spreadveränderung Corporate Bonds)
Wir setzen nun die MÖGLICHEN Rendite- und Spreadveränderungen (plus einem Korrektiv für die Defaults und Ratingveränderungen bei Corporate Bonds, wie oben beschrieben) in diese Formeln ein und erhalten für die beiden Anlageklassen ein Spektrum der theoretisch wahrscheinlichen Gesamterträge und Schwankungsbreiten (Volatilitäten). Dieser Ansatz berücksichtigt nicht nur die momentan niedrigen Kupons, sondern darüber hinaus auch die MÖGLICHEN Rendite- und Spreadveränderungen, wenn man realistischer Weise annimmt, dass Renditen und Spreads eine natürliche Untergrenze haben. Daraus lassen sich nun wieder Kombinationsportfolien nach obigem Muster (also 0% Treasuries/100% Corporate Bonds, 10%/90%, 20%/80%, usw.) und eine effiziente Grenze berechnen, die nun anders aussieht als beim historischen Ansatz:
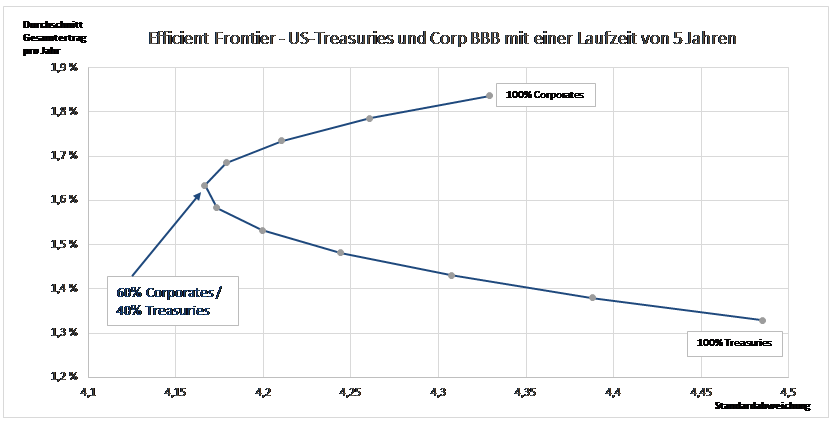
Ein risikoscheuer Investor müsste demnach nicht 20% in Treasuries und 80% in Corporate Bonds anlegen wie beim historischen Ansatz, sondern 40% in Treasuries und 60% in Corporate Bonds. Er rechnet im Prognosezeitraum (ein Jahr) unter diesem Ansatz nur noch mit einem veränderten durchschnittlichen Gesamtertrag von 1,63% und einer Standardabweichung von 4,17 %. Die Reduzierung des Anteils an Corporate Bonds – in unserem Beispiel von 80% auf 60% – ist vor Allem der Tatsache geschuldet, dass sich die Spreads dieser Corporate Bonds nun nicht mehr so deutlich einengen können, aber eben aufgrund ihres Ausfallrisikos genauso ausweiten können wie in der Vergangenheit (Stärkere Asymmetrie).
Klar ist aber auch, dass Corporate Bonds immer noch einen signifikanten Anteil in einem Anleiheportfolio einnehmen sollten, da sie die Volatilität des Gesamtportfolios reduzieren und dessen Rendite deutlich steigern können.
5. Anmerkungen zu Korrelationsannahmen
Zur Berechnung der wahrscheinlichen Renditen und Schwankungsbreiten für die beiden Anlageklassen haben wir oben sowohl historische als auch MÖGLICHE Rendite-und Spreadveränderungen (plus einem Korrektiv für die Defaults und Ratingveränderungen bei Corporate Bonds, wie oben beschrieben) in die Gesamtertrags-Formeln eingesetzt. Damit implizieren wir, dass sich die Korrelationen der Anlageklassen genauso verhalten wie in der Vergangenheit. Wir haben diese Methode gewählt, um im direkten Vergleich die Unterschiede zwischen dem auf historischen Renditen/Schwankungsbreiten basierten Ansatz und dem von uns bevorzugten Ansatz aufzuzeigen.
Die Korrelationsprognosen müssen aber nicht notwendigerweise aus der Vergangenheit abgeleitet werden. Man kann diese ebenso individuell festlegen wie die Renditeprognosen. Dies gilt auch für die Verteilungsfunktionen der Rendite- und Spreadveränderungen, die sich beispielsweise mit einer Monte-Carlo Simulation modellieren lassen, wodurch sich auch Korrelationsschwankungen, wie in der Praxis üblich, abbilden lassen. Darauf wollen wir in einem unserer nächsten Beiträge eingehen.
6. Fazit
Aus unserem Beispiel und dieser Analyse wird deutlich, dass aktuelle Marktbewertungen und -gegebenheiten unbedingt in die Ertragsprognose für die jeweiligen Anlageklassen einfließen sollten, um Fehlallokationen zu vermeiden. Dies gilt nicht nur für Anleihen, wo der Gesamtertrag klaren Rechenregeln folgt, sondern auch für andere Anlageklassen. Dort können beispielsweise relative oder historische Bewertungsmaßstäbe angelegt werden, um so eine Verschiebung hin zu realistischeren Ertrags- und Volatilitätswahrscheinlichkeiten und -verteilungen zu modellieren. Diese Methode wenden wir in der Beratungspraxis für die Prognose sämtlicher Anlageklassen an. Die daraus resultierenden Prognosen dienen uns als Grundlage für eine Asset-Allokations-Empfehlung.
Dieser Beitrag steht Ihnen auch als PDF-Download zur Verfügung: Renditeprognosen im Niedrigzinsumfeld
