Die verflixten Korrelationen in der Asset Allokation

März 2017

 

Um eine effiziente Verteilung der Anlagegelder („Asset Allokation“) auf die verschiedenen Anlageklassen (Aktien, Renten, etc.) vornehmen zu können, muss neben der Rendite für jede Anlageklasse auch die Wechselwirkung („Korrelation“) zu anderen Anlageklassen prognostiziert werden. Beide Prognosen, sowohl Rendite- als auch Korrelationsprognosen, gehen dann in die Berechnung einer effizienten Grenze („Efficient Frontier“) und eines optimalen (ex-anten) Investmentportfolios ein.

In der Praxis stellt die Prognosegenauigkeit für diese beiden Variablen aber eine große Herausforderung für jeden Investor dar. Zudem ist die Prognosegüte von Portfoliorendite und -risiko sehr anfällig gegen Prognosefehler bei diesen beiden Variablen. Viele Investoren scheuen daher die Prognose-Herausforderung und allokieren ihre Gelder lieber nach eher rudimentären Ansätzen.

Wie Renditen im heutigen Umfeld besser prognostiziert werden können, haben wir in unserem letzten Beitrag bereits gezeigt („Renditeprognosen im Niedrigzinsumfeld“).

In diesem Beitrag wollen wir uns mit der Frage der Korrelationsprognose beschäftigen. Dafür bedienen wir uns wieder eines einfachen Beispielportfolios aus Staats- und Unternehmensanleihen.

 

Inhaltsangabe

1. Einführung. 2
2. Historische Korrelationsanalyse. 2
3. Anforderungen an die Korrelationsprognose. 5
4. Copula-Funktionen. 5
5. Generelle Überlegungen zum Korrelationsumfeld. 6
6. Transformation zweier Zufallszahlenreihen. 7
7. Nichttechnische Beschreibung der Copula-Funktion. 8
8. Aus korrelierten Zufallszahlenreihen werden Verteilungs-/Dichtefunktionen. 10
9. Auswahl der entsprechenden Copula-Funktion. 13
10. Fazit. 15

 

1.     Einführung

In einem klassischen Beispiel der modernen Portfoliotheorie setzt sich ein illustratives Investmentportfolio sowohl aus Aktien eines Herstellers von Regenschirmen als auch aus Aktien eines Herstellers von Bademoden zusammen.

Dabei wird angenommen, dass bei gutem Wetter der Bademodenhersteller, bei schlechtem Wetter der Hersteller von Regenschirmen profitiert und sich dies jeweils in deren Gewinnen und Aktienkursen niederschlägt. Die Korrelation der beiden Aktien ist also negativ, so dass der Preisrückgang einer Aktie jeweils durch den Preisanstieg der anderen Aktie ausgeglichen wird.

Das Risiko – in unserem Fall als Schwankungsbreite des gesamten Portfoliowerts definiert - wird durch die negative Korrelation der beiden Aktien reduziert, ein Diversifikationseffekt für das Portfolio stellt sich ein.

Falls der Bademodenhersteller aber etwa auch bei schlechtem Wetter seine Bekleidung absetzen kann oder der Regenschirmhersteller auch bei strahlendem Sonnenwetter Regenschirme verkauft, verändert sich der Korrelationskoeffizient der beiden Aktien und damit auch der Diversifikationseffekt im besagten Investmentportfolio.

Um die mögliche Rendite und das Risiko eines Investmentportfolios zu prognostizieren, bedarf es neben der Renditeprognose für die einzelnen Anlageklassen also auch einer guten Korrelationsprognose, der somit eine wichtige Bedeutung in der Asset Allokation zukommt.

Nicht erst seit der Finanzkrise ist klargeworden, dass Korrelationen zum einen sehr instabil sind und zum anderen gerade dann „die Hilfe verweigern“ und gegen den Wert 1 tendieren, wenn sie am dringlichsten benötigt wird: in stark fallenden Märkten.

In diesem Beitrag wollen wir diese Problematik analysieren und Lösungswege aufzeigen.

 

2.     Historische Korrelationsanalyse

Im Folgenden wollen wir exemplarisch die historische Korrelation zwischen den zwei Anlageklassen untersuchen, die wir bereits im letzten Beitrag, („Renditeprognosen im Niedrigzinsumfeld“) verwendet haben:

-  5-jährige US-Staatsanleihen - nachfolgend „Treasuries“ genannt

- 5-jährige US-Unternehmensanleihen mit einem Rating von BBB/Baa - nachfolgend „Corporate Bonds“ genannt

Wenn wir im Folgenden „Treasuries“ oder „Corporate Bonds“ schreiben, meinen wir also immer diese beiden Anlageklassen mit den entsprechenden Ratings und Laufzeiten. Mit „Spreads“ meinen wir den Renditeaufschlag dieser Corporate Bonds über der Rendite dieser Treasuries.

Dabei betrachten wir nicht die Korrelation zwischen den absoluten Renditen und Spreads, sondern deren 1-Jahres Veränderungen (Veränderungen Corporate Bond Spreads rechts, inverse Skala):

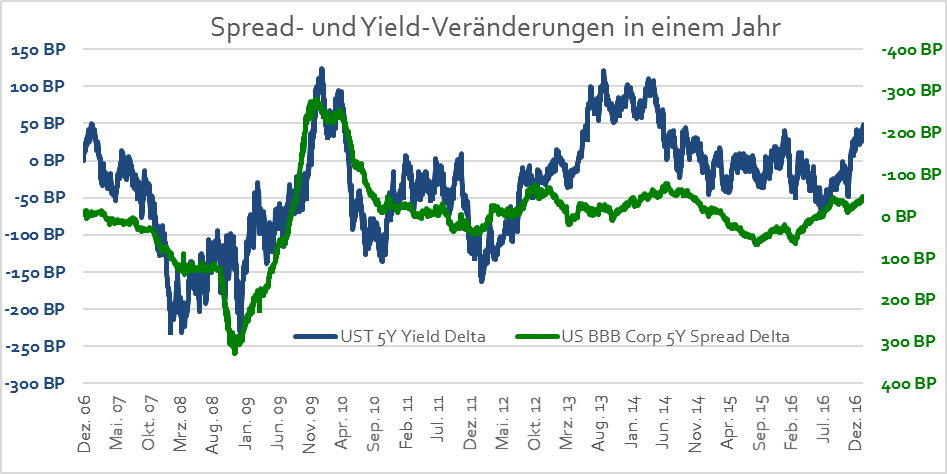
Die Korrelation zwischen der Spreadveränderung der Corporate Bonds und der Renditeveränderung der Treasuries messen wir in einem rollierenden 3-Monatszeitraum mit dem Pearson-Korrelationskoeffizienten, der zwischen -1 und +1 liegen kann[1]. Wenn wir im Folgenden von „Korrelation“ sprechen, meinen wir meist diesen Korrelationskoeffizienten.

Die Korrelation für die zwei Anlageklassen hat sich seit Anfang 2007 wie folgt entwickelt:

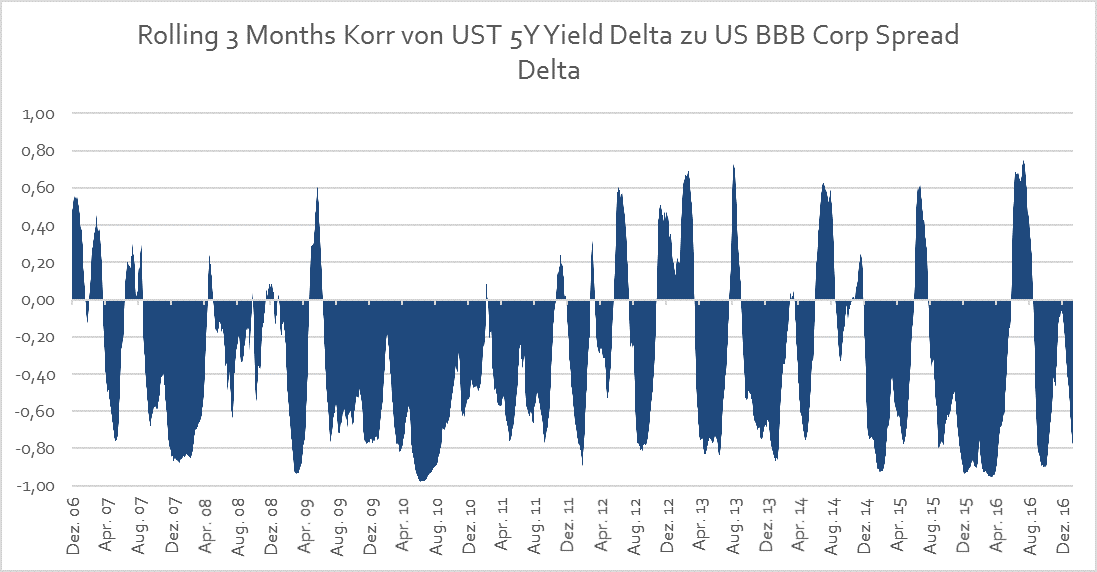
Die Korrelation der beiden Anlageklassen liegt für den gesamten von uns gewählten Zeitraum von Anfang 2007 bis Ende 2016 im negativen Bereich bei rund -0,61.

Dies entspricht auch den Erwartungen, denn in einem günstigen wirtschaftlichen Umfeld sollten fallende Spreads von Corporate Bonds in der Tendenz mit steigenden Renditen von Treasuries einhergehen und anders herum.

Beim Blick auf die beiden Schaubilder fällt allerdings auf, dass:

• die Korrelation sehr instabil ist und je nach Beobachtungszeitraum mehr oder minder stark schwankt
• die Korrelation in der extremen Phase der Finanzkrise 2008/2009 stark gegen -1 tendierte und in diesem Zeitraum - von 2007 bis 2011 – bei rund -0,75 lag
• der Beobachtungszeitraum mithin in zwei Phasen aufgeteilt werden kann: der Zeitraum der Finanzkrise von 2007-2011 in der die Korrelation relativ stabil bei rund -0,75 blieb und eine Erholungsphase von 2012-2016, in der die Korrelation wesentlich volatiler war und nur -0,31 betrug

Diese Beobachtungen bestätigt auch ein Blick auf ein Punkt-Schaubild, das auf der vertikalen Achse die Veränderung der Corporate Bond Spreads und auf der horizontalen Achse die Veränderung der Treasury-Rendite (in Basispunkten oder „BP“; 100 BP = 1,00%) abzeichnet:

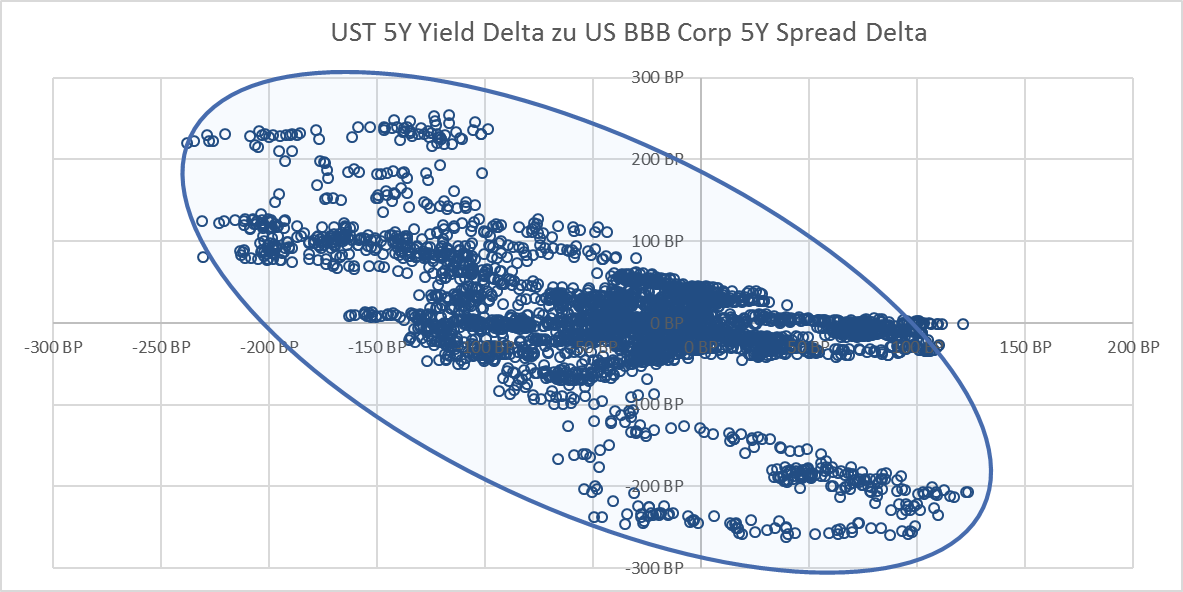
Bei extremen Veränderungen der Corporate Bonds Spreads haben sich auch die Renditen von Treasuries oft stark verändert. Die Korrelation dieser beiden Anlageklassen tendiert an diesen Extrempunkten stark gegen -1. Bei weniger starken Veränderungen der Corporate Bond Spreads fällt die Wechselwirkung zur Veränderung der Treasury-Renditen hingegen geringer aus, was durch die „unbestimmte Datenverdichtung“ („Datenknäuel“) nahe des Nullpunkts deutlich wird.

Diese Feststellung gilt nicht nur für das Anlageklassenpaar Corporate Bonds und Treasuries sondern für viele andere Anlageklassen. In extremen Märkten tendiert die Korrelation je nach Anlageklassenpaar oft gegen -1 oder 1, in weniger extremen Märkten hingegen eher gegen Null.

 

3.     Anforderungen an die Korrelationsprognose

Aufgrund dieser Beobachtungen wird deutlich, dass eine gute Korrelationsprognose drei Anforderungen erfüllen muss, wenn sie die Realität der Märkte abbilden möchte:

• für den festzulegenden Korrelationswert sollte das Stadium des Kreditzyklus berücksichtigt und daraus ein Korrelationsmuster abgeleitet werden. Für einen zu prognostizierenden Zeitraum bedeutet dies die Frage zu beantworten, ob beispielsweise das Korrelationsmuster von 2007-2011 oder eher das von 2012-2016 angewendet werden soll (oder das einer anderen Periode)
• der festzulegende Korrelationswert darf kein fixer („linearer“) Wert sein, sondern muss im Prognosezeitraum „schwanken“ dürfen, soll also nur über den gesamten Zeitraum, sozusagen „im Durchschnitt“, den festgelegten Wert erreichen
• der festzulegende Korrelationswert soll in extremen Märkten je nach Anlageklassenpaar gegen 1 oder -1 tendieren

Die in der modernen Portfoliotheorie („Markowitz-Ansatz“) und -praxis üblicherweise verwendete Mean-Variance-Optimierung erfüllt diese Anforderungen aber nicht. Denn sie nimmt für die Korrelation eines jeden Anlageklassenpaars einen bestimmten und fixen Wert („lineare Korrelation“) an, der sich über den Prognosezeitraum nicht verändert. Dieser wird meist aus Durchschnittswerten der Vergangenheit berechnet oder abgeleitet.

Dadurch werden:

• die unterschiedlichen Kredit-Zyklen und damit einhergehenden Korrelationsmuster nicht berücksichtigt
• die in der Realität beobachteten Korrelations-Schwankungen nicht abgebildet
• die in extremen Märkten gegen 1 oder -1 tendierenden Korrelationen nicht modelliert

 

4.    Copula-Funktionen

Ein festgelegter Wert für die Korrelationsprognose („lineare Abhängigkeitsstruktur“) kann, wie wir gesehen haben, die formulierten Anforderungen für eine Korrelationsprognose von Anlageklassen nicht erfüllen. Es bedarf also einer Matrix oder Funktion, die variabel genug ist um die Korrelations-Schwankungen und den Korrelations-Anstieg an den Extrempunkten über den Prognosezeitraum hinweg abzubilden.

In der Modellierung von Ausfallrisiken bei strukturierten Credit-Produkten (synthetische CDOs, etc.) haben sich seit Jahren bestimmte mathematische Funktionen etabliert, die sich auch in der Asset Allokation und in der Risikoanalyse zunehmender Beliebtheit erfreuen: Die Copula-Funktionen.

Die Copula-Funktionen erlauben es Abhängigkeiten bzw. Korrelationen unabhängig von der Wahrscheinlichkeitsverteilung jeder einzelnen Anlageklasse zu modellieren.

Im Folgenden soll in stark vereinfachter und nachvollziehbarer Weise dargestellt werden, wie wir mit diesen Funktionen Korrelationen zwischen den verschiedenen Anlageklassen modellieren.

Unser Demonstrationsportfolio besteht weiterhin nur aus Treasuries und Corporate Bonds.

 

a.      Generelle Überlegungen zum Korrelationsumfeld

Zunächst muss die Frage beantwortet werden, welches Korrelationsmuster angewendet werden soll bzw. welche Periode der Vergangenheit die Gegebenheiten des Prognosezeitraums am besten widerspiegelt.

Den von uns in der historischen Analyse (siehe oben) gewählten Zeitraum von 2007-2016 haben wir in zwei unterschiedliche Perioden eingeteilt:

• „Finanzkrisenzeit“ von 2007-2011: Die Korrelation lag bei -0,75 und war wenig volatil
• „Erholungsperiode“ von 2012-2016: Die Korrelation lag bei -0,31 und war sehr volatil

Welche dieser beiden Perioden spiegelt nun die Gegebenheiten für die nächsten zwölf Monate - unseren Prognosezeitraum - am besten wider?

Nun könnte man argumentieren, dass die hohen Bewertungen der Aktienmärkte, die hohe und zunehmende Verschuldung der Unternehmen, eine restriktivere Zentralbankpolitik und zunehmende politische Unsicherheiten mit einer Ausweitung der Corporate Bond Spreads und der Flucht in sichere Häfen (u.a. Treasuries) einhergehen werden. Dann würde man eher das Korrelationsmuster wählen, das der „Finanzkrisenzeit“ ähnelt, geringere Volatilitätsschwankungen annehmen und einen Korrelationswert von ca. -0,75 ansetzen.

Kommt man hingegen zum Schluss, dass die nächsten zwölf Monate auch weiterhin ohne größere Marktverwerfungen einhergehen werden, dann würde man eher das Korrelationsmuster wählen, das der „Erholungsperiode“ ähnelt, höhere Volatilitätsschwankungen annehmen und einen Korrelationswert von ca. -0,31 ansetzen.

Darüber hinaus können selbstverständlich noch andere Perioden der Vergangenheit als Referenz für den Prognosezeitraum herangezogen werden. Diese Überlegungen sollten von einem erfahrenen Marktbeobachter vorgenommen werden und sind wichtig.

Die „richtige“ Prognose des Korrelationswerts spielt unter einem Copula-Ansatz aber keine so große Rolle mehr wie im klassischen Markowitz-Ansatz. Denn im klassischen Markowitz-Ansatz stellt dieser Korrelationswert bereits die gesamte Korrelationsprognose dar. Unter einem Copula-Ansatz werden darüber hinaus, wie wir gleich noch sehen werden, auch die Korrelationsschwankungen und vor Allem die ansteigende Korrelation in extremen Märkten modelliert. Letztere spielt für den Diversifikationseffekt und die Reduzierung des Portfoliorisikos aber eine entscheidende Rolle. Prognosefehler für den Korrelationswert selbst haben unter einem Copula-Ansatz daher einen weitaus geringeren Effekt auf die Prognosegüte der Portfoliorendite und des Portfoliorisikos als im klassischen Markowitz-Ansatz.

Auch weil es uns hier nicht um eine konkrete Marktanalyse und Korrelationswertschätzung geht, wollen wir dieses Thema nicht weiter vertiefen und nehmen zu Demonstrationszwecken an, dass die nächsten zwölf Monate – unser Prognosezeitraum – eher der „Finanzkrisenzeit“ ähneln werden und durch einen hohen Korrelationswert und eine geringe Korrelationsvolatilität gekennzeichnet sind. Wir setzen daher -0,75 als Korrelationswert an.

 

b.     Transformation zweier Zufallszahlenreihen

In diesem Abschnitt wollen wir die Technik zum Aufbau einer Copula-Funktion beschreiben. Leser, denen eine weniger technische Beschreibung der Copula-Funktion ausreicht, können diesen Abschnitt überspringen und gleich zum nächsten Abschnitt „Nichttechnische Beschreibung der Copula-Funktion“ wechseln.

In einem ersten Schritt zur Erstellung einer Copula-Funktion werden für unser Beispiel (zwei Anlageklassen) zunächst zwei Zufallszahlenreihen generiert. Im Tabellenkalkulationsprogramm Excel lässt sich dies mit der Funktion „Zufallszahl“ umsetzen. So können beispielsweise zwei unabhängige Zufallszahlenreihen mit jeweils 10.000 Werten zwischen 0 und 1 generiert werden, die wir Zufallszahlenreihe 1 und Zufallszahlenreihe 2 nennen wollen.

Die beiden Zufallszahlenreihen sind in ihrer Häufigkeit jeweils (annähernd) gleichverteilt und weisen aufgrund ihrer Unabhängigkeit eine Korrelation von circa Null auf, was auch beim Blick auf ein Punkt-Schaubild deutlich wird:

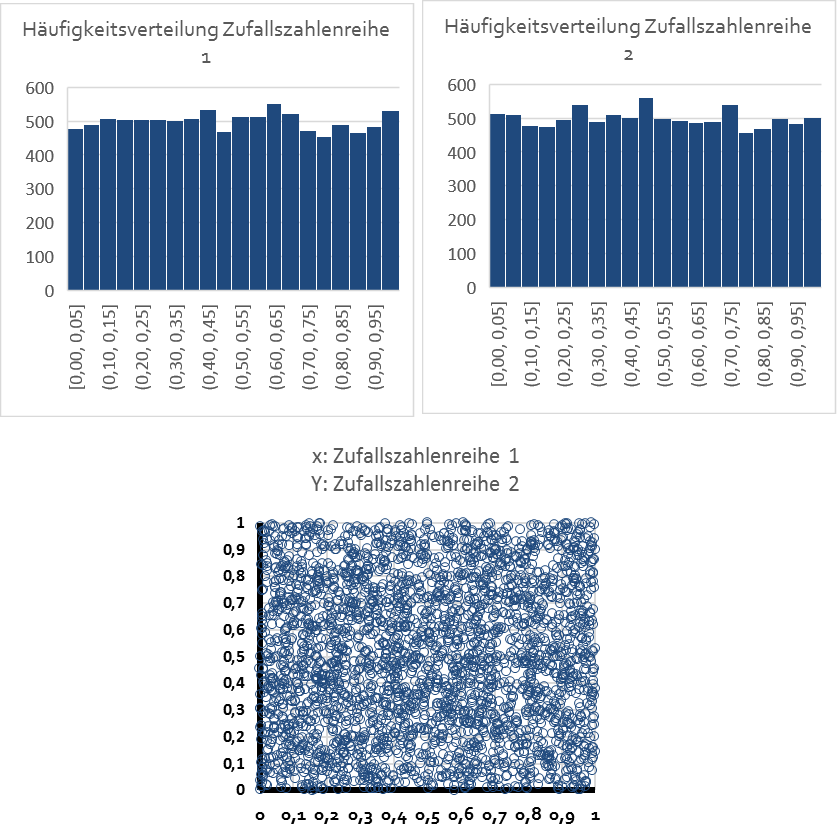
Im nächsten Schritt wird eine Korrelationsmatrix erstellt. Da wir in unserem Beispiel nur zwei Anlageklassen verwenden (Corporate Bonds, Treasuries), erstellen wir eine 2x2-Matrix und tragen dort den Korrelationswert ein, den wir im Abschnitt „Generelle Überlegungen zum Korrelationsumfeld“ mit -0,75 veranschlagt haben.

Nun erfolgt eine sogenannte (modifizierte) Cholesky-Zerlegung der Korrelationsmatrix. Die Cholesky-Zerlegung bezeichnet in der numerischen Mathematik generell eine Zerlegung einer symmetrischen positiv definiten Matrix in ein Produkt aus einer unteren Dreiecksmatrix und deren transponierten Matrix. Darauf wollen wir hier aber aufgrund der Sachfremdheit nicht weiter eingehen.

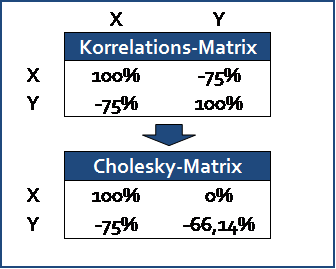
Unsere beiden Zufallszahlenreihen mit jeweils 10.000 Werten werden dann zunächst in zwei normalverteilte Zahlenreihen transformiert (in Excel mit der Funktion „Norm.Inv“), dann mit der modifizierten Cholesky-Matrix multipliziert und anschließend wieder in Zufallszahlenreihen umgewandelt (in Excel mit der Funktion „Norm.Vert“).

Mit dieser Cholesky-Zerlegung und der beschriebenen Multiplikation („Copula-Technik“) erzeugen wir aus einer linearen Abhängigkeitsstruktur eine funktionale Abhängigkeitsstruktur.

 

c.      Nichttechnische Beschreibung der Copula-Funktion

Die gerade beschriebene „Copula-Technik“ macht also aus zwei nicht korrelierten Zufallszahlenreihen zwei korrelierte Zufallszahlenreihen.

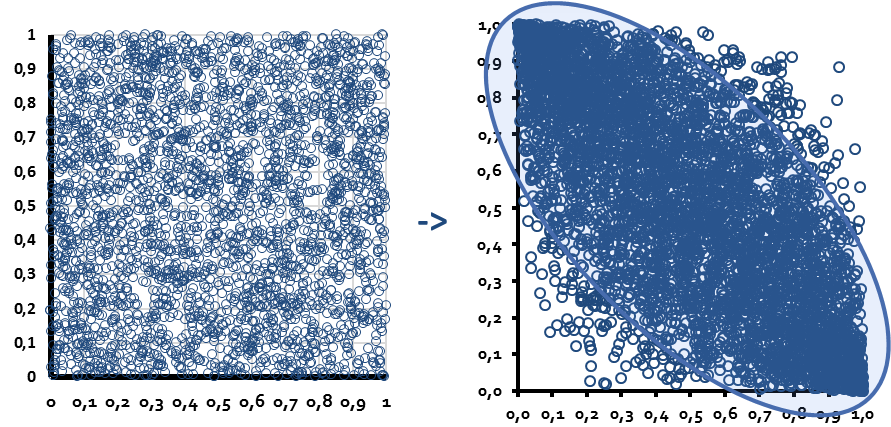
Die Korrelation der beiden Zufallsdatenreihen liegt nun (fast) genau bei dem Wert, der als Korrelationswert vorher festgelegt wurde: -0,75

Aus dem rechten Punktdiagramm wird aber deutlich, dass diese „Copula-Technik“ aus einem festen („linearen“) Korrelationswert eine flexible Korrelationsfunktion („Copula-Funktion“) gemacht hat, die die oben formulierten, gewünschten Anforderungen an eine Korrelationsprognose erfüllt:

• die in der Realität beobachteten Korrelations-Schwankungen werden abgebildet
• die in extremen Märkten gegen 1 oder -1 tendierenden Korrelationen werden modelliert

Denn an den Extrempunkten (beim Wert 1 und 0 unserer Zufallszahlen) verdichten sich die Datenpunkte im Punktdiagramm stark:

Ein hoher Wert einer Zufallszahlenreihe („hoher X-Wert“, nahe dem Wert 1) geht mit einem niedrigen Wert der anderen Zufallszahlenreihe („niedriger Y-Wert“, nahe dem Wert 0) einher und anders herum. Dies entspricht der Forderung, dass an diesen Extrempunkten der jeweiligen Datenreihen die Korrelation (für das zu modellierende Anlageklassenpaar Corporate Bonds und Treasuries) stark gegen den Wert minus eins tendiert. In der Mitte des Punkt-Diagramms ist die Korrelation aber deutlich geringer und tendiert eher gegen Null, wie auch die deutlich geringere Datenpunktkonzentration dort zeigt. Über alle Datenpunkte hinweg entspricht die Korrelation aber (fast) genau dem Wert, den wir vorher festgelegt haben: -0,75

Jede unserer zwei Zufallszahlenreihen für sich weist aber weiterhin die Eigenschaften einer „normalen“ oder „unbehandelten“ Zufallszahlenreihe auf: Die Häufigkeiten sind (annähernd) gleichverteilt und der Mittelwert liegt weiterhin bei jeweils ca. 0,5:

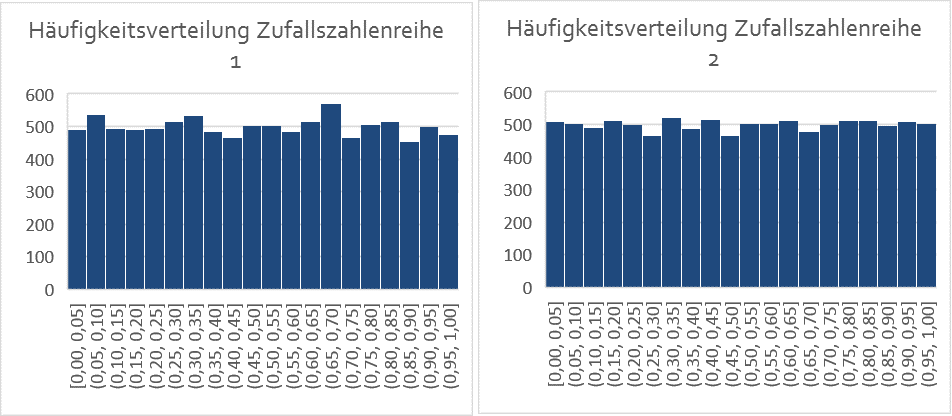
Mit diesen beiden korrelierten Zufallszahlenreihen kann nun für jede Anlageklasse individuell eine Verteilungs- bzw. Dichtefunktion generiert werden, ohne dass dabei die gerade geschaffene Abhängigkeitsstruktur („Korrelationsfunktion“ oder „Copula-Funktion“) zwischen den beiden Anlageklassen verändert wird.

 

d.     Aus korrelierten Zufallszahlenreihen werden Verteilungs-/Dichtefunktionen

 

Im nächsten Schritt werden nun also die beiden korrelierten Zufallszahlenreihen (Zufallszahlenreihe 1 und 2) jeweils zur Modellierung der Rendite- und Spreadveränderung von Treasuries und Corporate Bonds verwendet.

Nimmt man beispielsweise an, dass die Renditeveränderungen von 5-jährigen Treasuries normalverteilt sind, einen Mittelwert von 0 Basispunkten und eine (jährliche) Standardabweichung von 100 Basispunkten (1,00%) haben, so kann diese Verteilung der Renditeveränderung mit unserer Zufallsdatenreihe 1 und der Funktion „Norm.Inv“ im Tabellenkalkulationsprogramm Excel unter Eingabe der entsprechenden Parameter erzeugt werden:

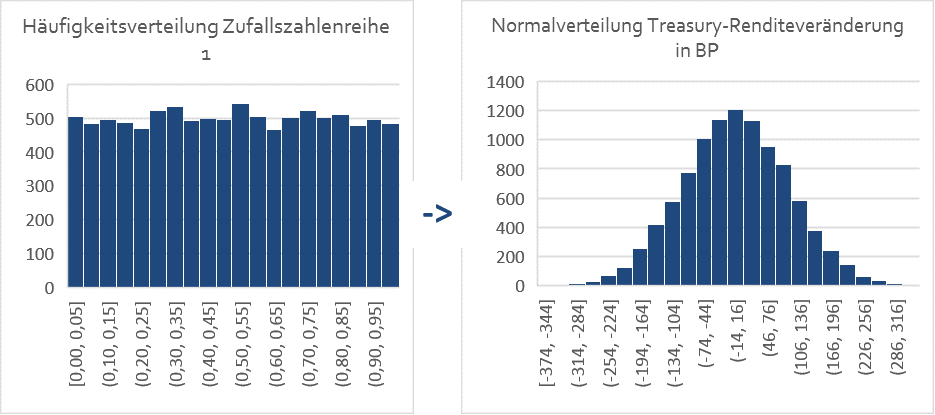
Dasselbe gilt für die Zufallszahlenreihe 2 und die Corporate Bond Spreads.

Im unserem letzten Beitrag („Renditeprognosen im Niedrigzinsumfeld“) haben wir allerdings aufgezeigt, dass insbesondere Spreadveränderungen von Corporate Bonds im heutigen Niedrigzinsumfeld nicht mehr normalverteilt sind, sondern eine einseitige Verteilung („rechtsschief“) aufweisen.

Kein Problem! Denn mit unserer Zufallszahlenreihe 2 können wir auch eine solche einseitige Verteilung der Corporate Bond Spreads, beispielsweise unter Zuhilfenahme der Excel-Funktion „Beta.Inv“ und Eingabe der entsprechenden Parameter (Spreadveränderung Obergrenze, Untergrenze, Schiefe, etc.), in Excel erzeugen und so die heute im Niedrigzinsumfeld noch möglichen Spreadveränderungen bei Corporate Bonds modellieren:

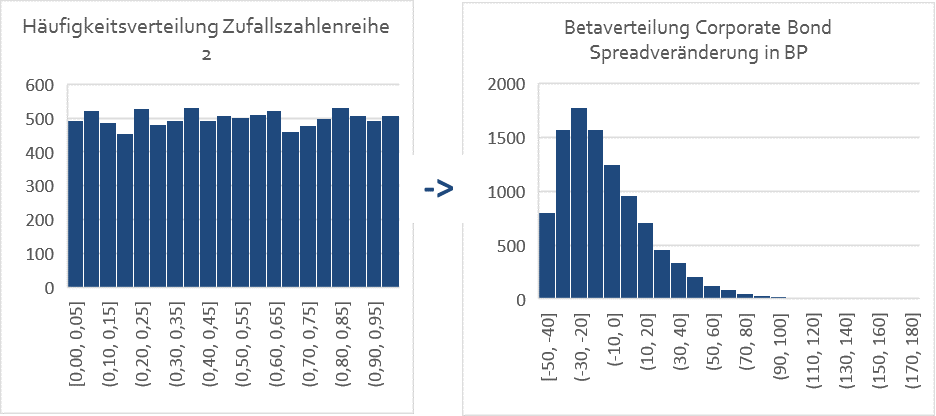
Da unsere zu Grunde liegenden Zufallszahlenreihen (Zufallszahlenreihen 1 und 2) über die oben erzeugte und beschriebene Copula-Funktion korreliert sind, sind nun auch die aus diesen Zufallszahlenreihen hervorgegangenen Verteilungen für die Veränderungen der Corporate Bond Spreads und der Treasury-Renditen über dieselbe Copula-Funktion korreliert.

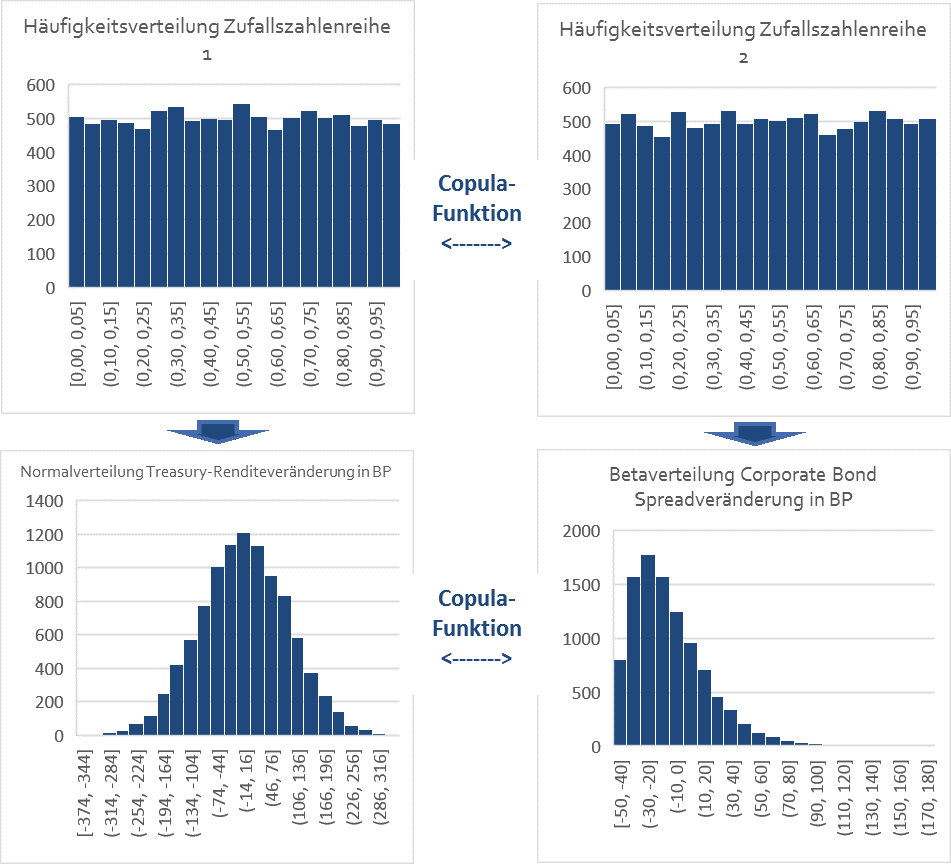
Und diese Korrelation zwischen den beiden Anlageklassen ist eben nicht durch einen fixen („linearen“) Korrelationswert definiert, sondern durch eine flexible Korrelationsfunktion („Copula-Funktion“), die ebenfalls die oben formulierten Anforderungen an die Korrelationsprognose erfüllt:

• die in der Realität beobachteten Korrelations-Schwankungen werden abgebildet
• die in extremen Märkten gegen 1 oder -1 tendierenden Korrelationen werden berücksichtigt

Unsere modellierte Korrelationsfunktion zwischen den Zufallszahlenreihen 1 und 2 - und damit eben auch zwischen den Veränderungen der Corporate Bond Spreads und der Renditeveränderung von Treasuries - entspricht also, was das Korrelationsverhalten angeht, dem beobachteten Verhalten dieser Anlageklassen in der Realität:

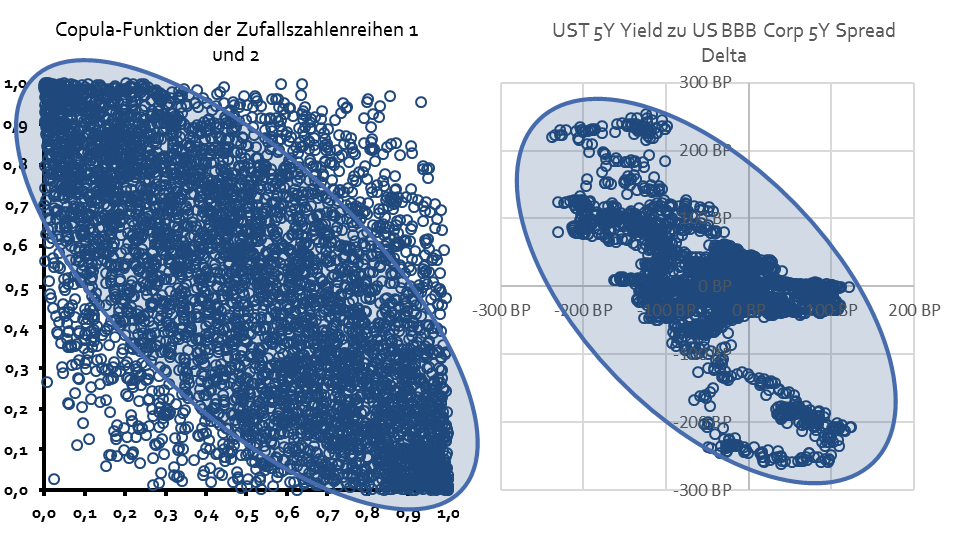
Damit verfügen wir für die beiden Anlageklassen Treasuries und Corporate Bonds über eine Korrelationsprognose in Form einer Copula-Funktion.

Darüber hinaus verfügen wir ja auch über die Verteilungen der Veränderungen von Treasury-Renditen (normalverteilt) und Corporate Bond Spreads (Betaverteilt), die wir soeben modelliert haben:

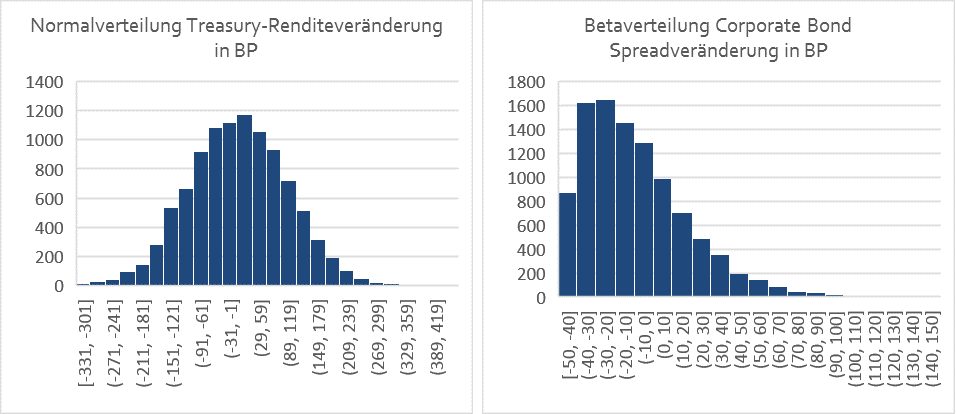
Daraus lassen sich nun - wie in unserem letzten Beitrag („Renditeprognosen im Niedrigzinsumfeld“) bereits aufgezeigt - Rendite- und Volatilitätsprognosen und eine effiziente Grenze („Efficient Frontier“) für das Gesamtportfolio berechnen. Und diese Rendite- und Volatilitätsprognosen verbindet dieselbe Copula-Funktion, die auch die Spread- und Renditeveränderungen korreliert.

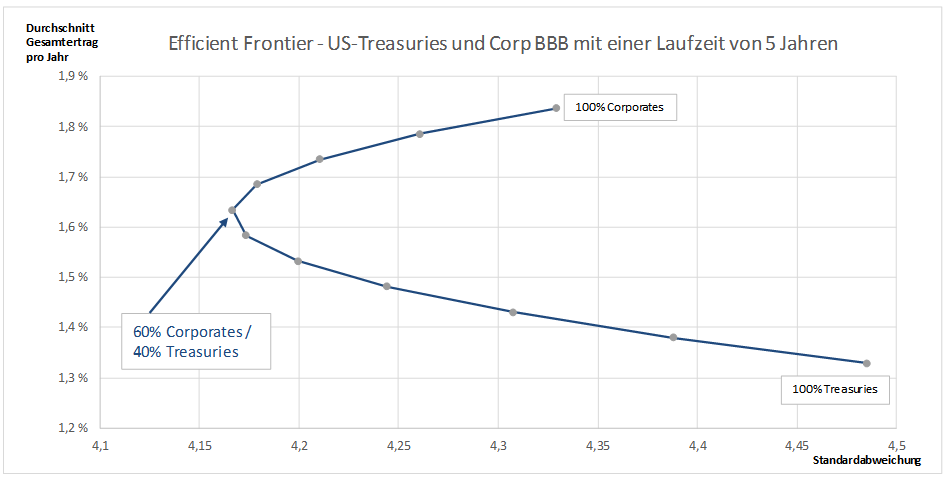
Auf die Erstellung der Rendite- und Volatilitätsprognosen und die Berechnung der effizienten Grenze wollen wir hier aber nicht weiter eingehen, da wir dies bereits im besagten letzten Beitrag getan haben.

Auf Basis dieser errechneten effizienten Grenze kann der Investor nun eine (ex-ante) optimale Asset Allokations-Entscheidung treffen.

In unserem Beispiel besteht unser Portfolio zwar nur aus zwei Anlageklassen: Treasuries und Corporate Bonds. Selbstverständlich gilt der hier beschriebene Ansatz aber auch für alle anderen Anlageklassen (Aktien, Währungen, Rohstoffe, Immobilien, etc.) und sollte darauf Anwendung finden.

 

e.      Auswahl der entsprechenden Copula-Funktion

Wir haben bisher nur von einer (bisher nicht weiter spezifizierten) Copula-Funktion gesprochen und aufgezeigt, wie diese erzeugt und angewendet wird. Bei der von uns oben verwendeten Copula-Funktion handelt es sich um die Gauß- oder Normal-Copula-Funktion.

Darüber hinaus gibt es aber noch viele weitere Copula-Funktionen, die sich generell in zwei Gruppen unterteilen lassen:

• Elliptische Copulas (Normal, Student-t, etc.)
• Archimedische Copulas (Gumbel, Clayton, etc.)

Beide Gruppen unterscheiden sich, vereinfacht ausgedrückt, durch eine unterschiedliche Symmetrie/Asymmetrie der Datenpunkte. Darauf wollen wir hier aber nicht weiter eingehen.

Etwas genauer wollen wir uns aber noch den Unterschied zweier elliptischer Copula-Funktionen, der Normal Copula-Funktion und der Student-t Copula-Funktion, anschauen:

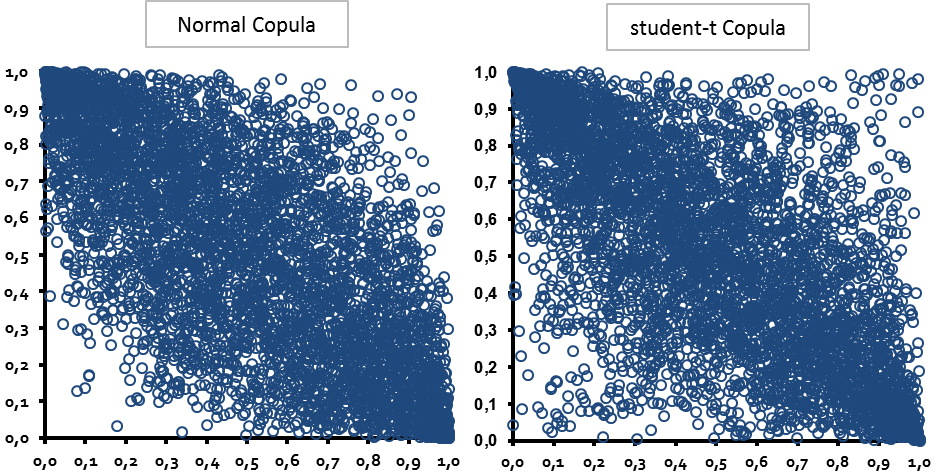
Bei sehr hohen Freiheitsgraden konvergiert die Student-t Copula-Funktion (rechtes Schaubild) zu einer Normal-Copula-Funktion (linkes Schaubild). Bei niedrigen Freiheitsgraden, wie wir sie hier verwendet haben, weist die Student-t-Copula-Funktion aber eine größere Streuung der Datenpunkte an den Nicht-Extrempunkten - und damit eine höhere Korrelationsschwankung - innerhalb des Beobachtungs- oder Prognosezeitraums auf.

Im obigen Abschnitt „Generelle Überlegungen zum Korrelationsumfeld“ haben wir prognostiziert, dass die Korrelationsschwankungen in den nächsten zwölf Monaten eher der Periode von 2007-2011 ähneln dürften („Finanzkrisenzeit“) und daher gering ausfallen sollten. Den Korrelationswert haben wir sodann mit -0,75 angesetzt und eine Normal-Copula-Funktion generiert und verwendet.

Kommt man bezüglich des Korrelationsumfelds für die nächsten zwölf Monate hingegen zu einer anderen Einschätzung und nimmt eine höhere Korrelationsschwankung an, dann könnte man in diesem Fall anstelle einer Normal-Copula auch eine Student-t-Copula verwenden, die eben diese höheren Korrelationsschwankungen besser widerspiegelt.

Aber auch darauf wollen wir hier nicht näher eingehen, sondern nur darauf hinweisen, dass zu einer generellen Überlegung über das Korrelationsumfeld letztendlich auch die Auswahl einer geeigneten Copula-Funktion gehört, die die Gegebenheiten des Prognosezeitraums vor Allem im Hinblick auf die Korrelationsschwankungen am besten widerspiegelt.

 

5.     Fazit

Die Berechnung einer effizienten Grenze („Efficient Frontier“) und eine qualifizierte Asset Allokations-Entscheidung erfordern im Wesentlichen eine quantitative Prognose für diese drei Variablen:

• Renditen der einzelnen Anlageklassen (Aktien, Renten, etc.)
• Volatilitäten der einzelnen Anlageklassen
• Korrelationen zwischen den Anlageklassen

Wie wir die Renditen und Volatilitäten der einzelnen Anlageklassen prognostizieren und berechnen, haben wir bereits in unserem letzten Beitrag („Renditeprognosen im Niedrigzinsumfeld“) aufgezeigt und uns in diesem Beitrag der letzten Variable, der Korrelationsprognose, gewidmet.

Die Erfahrungen aus der Finanzkrise zeigen, dass eine gute Korrelationsprognose drei Bedingungen erfüllen muss:

• für den festzulegenden Korrelationswert sollte das Stadium des Kreditzyklus berücksichtigt und daraus ein Korrelationsmuster abgeleitet werden.
• der festzulegende Korrelationswert darf kein „fixer“ („linearer“) Wert sein, sondern muss im Prognosezeitraum schwanken dürfen
• der festzulegende Korrelationswert soll in extremen Märkten je nach Anlageklassenpaar gegen 1 oder -1 tendieren

Wir haben in diesem Beitrag gezeigt:

• wie ein Korrelationsmuster abgeleitet oder prognostiziert werden kann
• dass eine Korrelationsprognose am besten über eine Copula-Funktion erfolgen sollte
• dass solche Copula-Funktionen die geforderten Bedingungen besser erfüllen und (ex-ante) zu einer besseren Asset Allokationsentscheidung führen, als dies mit dem traditionellen Mean-Variance-Ansatz („Markowitz-Ansatz“) möglich ist
• die Prognosegüte mit diesem Copula-Ansatz weniger anfällig gegenüber Prognosefehlern bei Korrelationswerten selbst ist

Der Aufwand für eine solche Prognose von Renditen, Volatilitäten und Korrelationen ist nicht zu unterschätzen. Unseres Erachtens löhnt es sich aber diesen Aufwand zu betreiben, da daraus in der Regel eine bessere Asset Allokationsentscheidung resultiert und die ansonsten verdeckt bleibenden, implizierten Annahmen eines rudimentären Ansatzes aufgedeckt und überdacht werden können.

 

Dieser Beitrag steht Ihnen auch als PDF-Download zur Verfügung: Die verflixten Korrelationen in der Asset Allokation

 

[1] In diesem Beispiel haben wir die Corporate Bond Spreads aus Vereinfachungsgründen und zu Demonstrationszwecken nicht um Ausfälle und Ratingveränderungen (Defaults/Downgrades) bereinigt, in der Analyse und Beratungspraxis nehmen wir diese Korrekturen aber vor, wie auch in unserem letzten Beitrag „Renditeprognosen im Niedrigzinsumfeld“ dargestellt.